正規分布
正規分布(normal distribution)は連続型の確率分布で、代表的かつ最も重要な分布である。離散型ではないので分布のグラフはヒストグラムではなく曲線で描かれる。ガウス分布(Gaussian distribution)ともいう。ガウスが統計学の分野で誤差分布として正規分布を提唱した業績によるものと思われる。正規分布という名前で呼んだのはピアソンらしい。ピアソンはこの命名を後に後悔したというが、すでに定着してしまった。正規分布の発見はガウスやピアソンよりも古い。
下図が正規分布曲線で、その形状から西欧では「ベル型の分布」と比喩されることが多い。ベルを日本語に翻訳して釣鐘型ということがあるが、もしも、ベルの日本語訳としてではなく、日本の寺にある釣鐘を連想すると誤解することになる。日本の寺の釣鐘は裾を引いておらず、欧米の教会のベルとは異なるからである。
正規分布の確率密度関数は以下の通りで、μとσが母数で、それぞれ期待値(平均)と分散である。このふたつの母数によって正規分布の形が決まる。
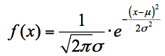
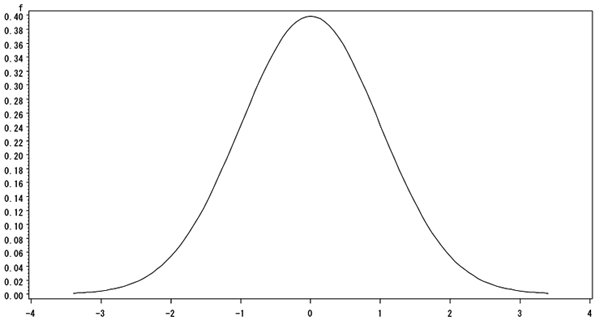
μ=0、σ=1の場合を特に標準正規分布といい、確率密度関数は以下の通り。上図はxの値として、-3.4から+3.4まで0.2刻みで与えた時のfの値を結んで描いた標準正規分布の曲線である。
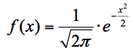
無限小から無限大までのx座標(横軸)と曲線の下に囲まれた面積は全体で1であり、全事象の起こる確率が1であることにに対応する。
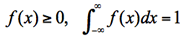
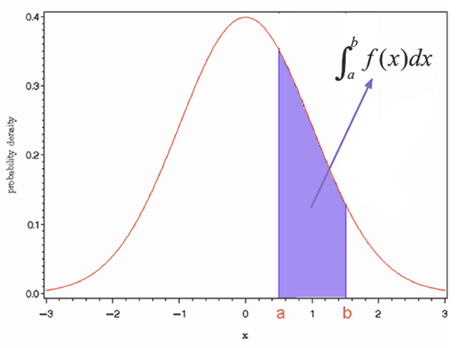
正規分布は連続分布なので、さまざまなxの値の範囲と確率が対応する。下図は区間(a,b)の面積が確率に対応する様子を示した。
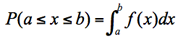
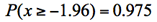
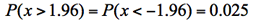
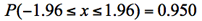
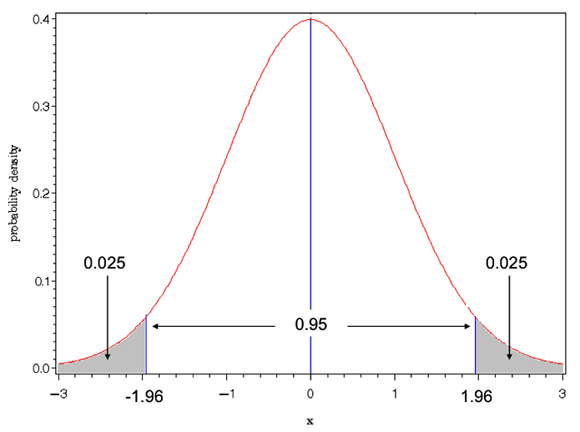
<どこで、どのように使うのか>
正規分布とは何の分布で、どうして重要なのか。ガウスは観測値の誤差の分布として発見した。
たまに統計学のテキストにおける正規分布の説明で、身長等の分布形が正規分布に似ている例として掲載されているが、このような観測度数のヒストグラムと結び付けない方が良い。誤解するだけである。
正規分布はあくまでも理論的な確率分布である。調査で身長など自然現象を観察した時の度数分布が似ているということではない。ではなにか?
たとえば「日本人の成人」という母集団(約1億人)から500人を無作為抽出して標本調査を実施して、身長の標本平均(n=500)を得た。この標本平均という標本統計量が正規分布するのである。500人の個々の身長という観測値の度数分布が正規分布に似ていることではなく、500人の平均身長が正規分布するのである。この区別ができれば、確率分布の理解が始まったことになる。
1億人から500人を復元単純無作為抽出した標本は「1億の500乗」個ある。この無数に近い標本平均について重要な性質は
1.平均身長の平均値mの平均(期待値)E(m)は、母平均μに一致する
2.平均身長mの分散σ2/nである
3.平均身長mは近似的に正規分布する
<中心極限定理>
正規分布が重要な理由のひとつに、中心極限定理がある。
「平均μ,分散σ2の分布をもつ母集団から,無作為標本を抽出すると,標本平均mの分布は,標本サイズnが増大するにつれて,平均μ,分散σ2/nの正規分布に近づく」
(中心極限定理)
ほとんどの母集団において中心極限定理が成立する。「ほとんど」というのは、分散を持たない母集団などの例外(コーシー分布など)を除いて、ということである。
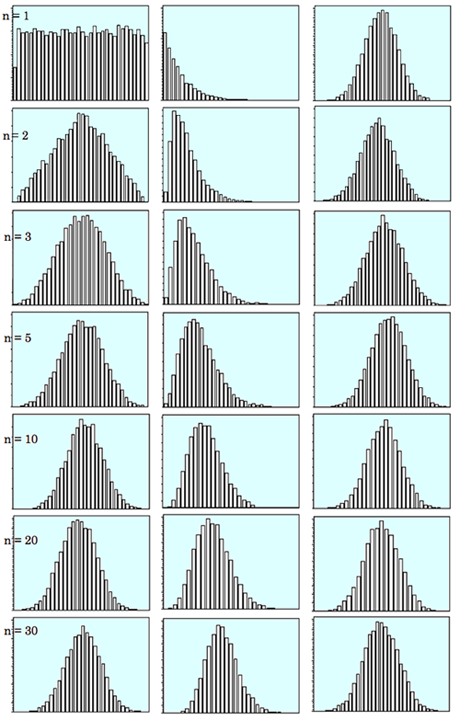
母集団が正規分布している場合はもちろんだが、驚くべきことに、母集団が一様分布であろうと、指数分布であろうと、標本平均は漸近的に正規分布するのである。
下図の3列は、それぞれ左から一様分布,指数分布,正規分布である。標本サイズ(n)の大きさを、1, 2, 3, 5, 10, 20, 30と次第に大きくしている。漸近的に正規分布する様子が分かる。
中心極限定理を誤解して、「標本サイズを大きくしていけば、どんなデータでも正規分布する」との説明を見たことがある。誤解か不十分な定理表明である。所得分布は正規分布していない。全数調査をしても正規分布していない。これはすぐに理解できるだろう。しかし平均所得は正規分布に漸近するのである。無作為抽出する限りにおいて。