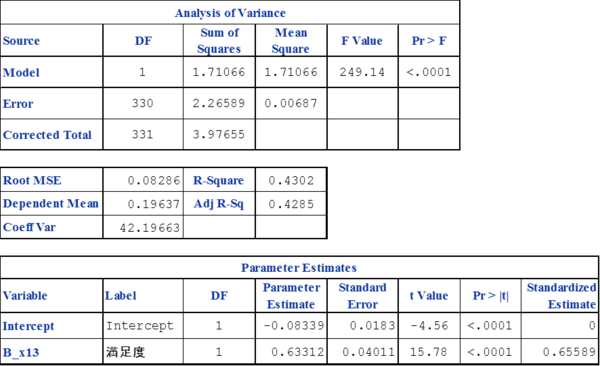
単回帰分析
回帰分析(regression analysis)は予測のための手法として利用されることが多い。たとえば売上高を予測したい等、ビジネスの未来の予測をしたい場面は多い。さらに予測を実現するためには、どこを動かせば効果的なのかも知りたい。
売上高など目的とする指標のことを、回帰分析では目的変数という。売上高を高めることに影響している要因は、業務知識等から候補を考えることができるだろう。予測に影響を与える指標のことを説明変数という。統計モデルとしては説明変数によって目的変数を予測するという定式化をする。

マーケティング調査では目的変数として、売上高のような財務データだけでなく、広告注目率、総合満足度、購入意向率などを目標指標とすることも多い。そのほか選挙予測調査において当選者の得票率予測、政党別の獲得議席数予測などでも利用されている。回帰分析は多変量解析の中でも非常に応用範囲の広い手法である。
回帰分析の使い方としては、予測の精度を高めたいということのほかに、どの説明変数が目的変数に強い影響力を持っているかを知りたい。これは予測分析というより要因分析の性質が強いが、回帰分析で両方の結果を得ることができる。
説明変数が1個の回帰モデルを単回帰分析(simple regression analysis)、複数の回帰モデルを重回帰分析(multiple regression analysis)という。単回帰分析には回帰分析を理解するうえでの基本的な内容がほとんど含まれている。重回帰分析はその拡張である。回帰分析を理解するうえで相関係数に関する知識を持っているとよい。相関と回帰の相違を考えると理解が容易になる側面があるからである。
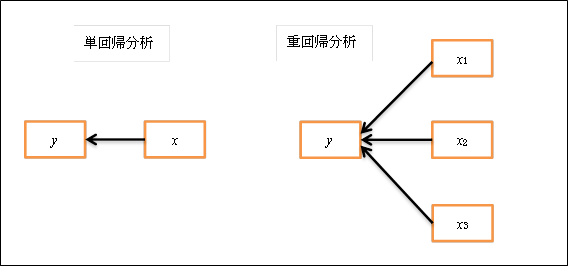
- 予測力の良さの指標として、説明変数で目的変数を何割くらい説明しているかという説明率を計算することができる。これを決定係数という。
- 目的変数を予測するのに、どの説明変数の影響が強いのかを計算することができる。これを寄与率という。上図の矢印を回帰係数というが、寄与率は回帰係数の値の大きさと関係している。
<単回帰分析の例>
日経リサーチのブランド戦略サーベイのデータの一部を使って単回帰分析をした。購入意向を目的変数とし、満足度を説明変数とする単回帰分析である。満足度の向上が購入意向を高めるというモデルである。
分析結果として一般に以下のような出力結果(SASによる分析結果)が得られる。
決定係数はR-Squareの欄に出ており、43%であることが分かる。R-Squareは重相関係数の平方(2乗)という意味である[1]。回帰分析における決定係数は重相関係数の二乗であるが、単回帰分析の場合は単に相関係数の二乗である。
回帰係数はParameter Estimatesの欄にあり、0.63であることが分かる。ここから単回帰モデルは下式のような直線の式になる。購入意向がyで、満足度がxである。満足度を1単位高めると、購入意向を0.63だけ向上させると解釈できる。
y=-0.083+0.633x
回帰係数には、変数を標準化した場合の標準化回帰係数がある。Standardized Estimateの欄に、0.656と示されている。単回帰分析の場合は、説明変数が1個しかないので、
- 標準化回帰係数は相関係数と等しい。(0.65589)
- 標準化回帰係数(相関係数)の平方と、決定係数(重相関係数の平方)は等しい。( 0.65589 )2 = 0.4302
<分析結果表の説明>
この他にも関連する分析結果が出るが、出力表の見方が分かると理解も深まることもあるので、一つひとつの数値の意味を確認してみる。回帰分析は歴史も長く、利用者も多いため、ほとんどの統計ソフトウエアで同じ出力形式である。
最初に分散分析表(Analysis of Variance)が出てくる。なぜ分散分析表が出るのかというと、データの「分散」を分析しているからである。どういう意味か。多くのデータ解析の根底には、現象(Data)を構造(Model)と差異(Error)に分解するという思想が横たわっている。西欧哲学の構造主義と根底は同じである。分析しようとしている現象の、何が構造の系であり、何が差異の系であるかを見出すこと。それがデータ解析の場合はデータの分散を、モデルの部分と、誤差の部分に分解することに対応する。
Data = Model + Error
データの分散は「情報」であり、この例では「購入意向」を「満足度」で説明できる部分(Model)と、それ以外(Error)とに分離・分解しているのである。
分散分析表には目的変数である購入意向の「分散」(表の平方和:Sum of Squaresの列)が3.97655であることが示されており[2]、ここに直線の式、つまり回帰モデルを当てはめて計算すると、Modelの平方和が1.71066となった、と示している。
3.97655 = 1.71066 + 2.26589
隣の列は平方和を自由度(DF)で割った平均平方(Mean Square)である。平均平方が分散に相当する。平均平方のモデルと誤差の比がF値(F value)である。F値のことを分散比とかF比というのはこのためである。
F = 249.14 =1.71066 / 0.00687
という関係になっている(下位桁は丸め誤差のため一致しない)。その横にF検定の結果としてP値が示されている。高度に有意であり、この回帰モデルは意味があると解釈される。
その下の表には誤差の平均平方の平方根(Root MSE)が 0.08286 と出力されている。RMSEは誤差の標準偏差である。回帰モデルによる予測に関する統計的推測で使う。
また購入意向の平均値(Dependent Mean)と変動係数(Coef Var)も示されている。Dependentとは従属変数という意味であるが、目的変数のことである。分野によって変数の呼び方は多種多様である[3]。
その横に決定係数が示されている。自由度調整済み決定係数(Adj R-Sq)も算出されているが、単回帰分析の場合は無意味なので無視すればよい。
最後に母数の推定値(Parameter Estimates)が出力される。単回帰分析なので切片(Intercept)と説明変数(満足度)の2行のみである。回帰係数をt検定するために、標準誤差(Standard Error)とt値およびP値が算出されている。高度に有意であり、回帰係数は意味がある。なお、単回帰分析の場合は説明変数が1個だけなので、このt検定とモデル全体のF検定は同値である。標準化回帰係数の列では、切片が0になっている。標準化するということは、変数の平均0、分散1なので、直線は原点を通過する。
<直線の当てはめ>
単回帰分析は幾何学的には、目的変数(y)と説明変数(x)の散布図に、直線を当てはめることである。どのように当てはめるかという基準が必要だが、概念的には「全データをよく代表するように」という考え方である。
代数的には下の直線の式[4]の切片(b0)と傾き=回帰係数(b1)を求めることである。切片と回帰係数が推定すべきパラメータ(母数)である。
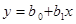
そこで下式のような誤差項(e)を含む統計モデルを考える。
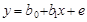
数理的には個々の観測値(i)と直線との差(ei)の二乗和(Se)を最小化するように定める。このような方法を最小二乗法という。「全データをよく代表する」基準として、最小二乗基準を採用しているということになる。直線と観測値との差は幾何学的には、直線への垂線の長さである。これを数理的には「残差」ともいう。
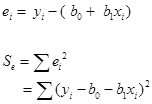
微分の知識が必要だが、最終的に下の公式が得られる。単回帰係数は「目的変数と説明変数の積和」と「説明変数の平方和」との比である。実際には手計算は面倒なので、統計ソフトウエアを使うが、単回帰分析を利用する立場としては算出の考え方を理解しておこう。
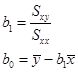
<単回帰分析と相関係数>
単回帰係数(b1)と相関係数(r)の関係は、以下のようになっている。
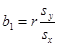
つまり単回帰係数は、目的変数と説明変数のそれぞれの標準偏差(syとsx)の比と、相関係数の積である。従って、変数が標準化されている場合は、単回帰係数と相関係数は一致することが分かる。
相関係数においては二つの変数の関係は対称である。しかし回帰分析の場合、目的変数と説明変数を入れ替えると、回帰係数の値は同じにはならない。「yのxへの回帰」と「xのyへの回帰」は異なる結果になる。
<回帰という用語について>
Darwinの従兄弟であるGalton(1822-1911)はNatural Inheritance (1889) の中で親の身長と子供(成人)の身長のデータ(928組)を示している。Galtonはこのデータを分析した結果から「身長の高い親の子の平均は、親程には高くない。身長の低い親の子の平均は、親程には低くない」との知見を得て、「平均から遠い親の子の身長は、集団の平均に回帰する」と考えた。これは相関係数が1でない限り当然の数学的現象(これを今では回帰効果という)に過ぎないが、Galtonはここで平均への回帰(regression)という概念を登場させ、そこから回帰分析という名称が使われることになった。
回帰分析は「xからyを予測する」のだが、回帰という場合は「yのxへの回帰」という。逆ではないかと間違えやすいが、regressionという発想に至った歴史的起源を考えるとよい。
[1] 平方和と二乗和(自乗和)は同じ意味である。平方は幾何学的な、二乗は計算的なイメージである。自乗と書き「じじょう」と読むが、二乗は自分と自分の積なので、自分に自分を乗せるという感覚による。
[2] 平方和の平均が分散であるが、ここでは「分散」を広い意味でデータの変動の指標としている。変動の指標には、平方和、分散、標準偏差、変動係数などがある。
[3] 目的変数と説明変数のほか、数学では「従属変数-独立変数」、経済学では「内生変数-外生変数」などという。目的変数を「基準変数」「応答変数」、また説明変数は「予測変数」「原因変数」などもいう。背景や分野の相違に過ぎない。
[4]中学校の数学では、直線の式は「y = ax + b」と学ぶが、回帰分析では説明変数が多数になるということもあって、切片を最初に置く。混乱を避けるためと、行列式表現なども考慮し、切片も傾きも共通にbを使い、添字で区別する。