バリマックス回転
因子分析における直交回転法のひとつで、もっともよく利用されてきた。回転の目的は因子の解釈を容易にすることであり、バリマックス回転(varimax rotation)が解釈しやすい結果を与えることが多かったために、研究者や実務家に非常に頻繁に利用されてきた。実は回転方法は無数にある。
素朴な疑問として「回転」とは何なのか、なぜ「回転」するのか、ということを理解したいが、それに先立って回転前(初期解)と回転後(回転解)の実例を示す。これはブランド戦略サーベイの企業イメージ25変数の因子分析である。どのような変化が回転前後で生じているであろうか。
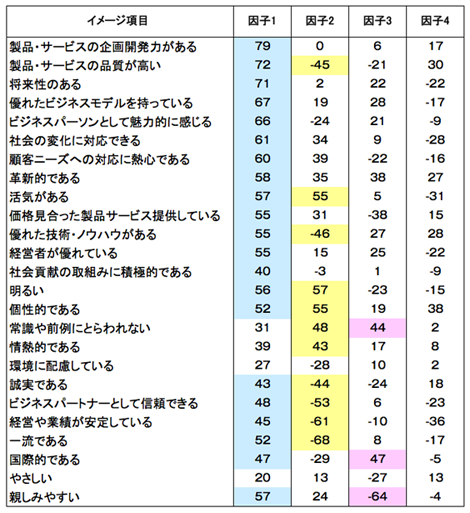
バリマックス回転後(回転解)の因子負荷行列
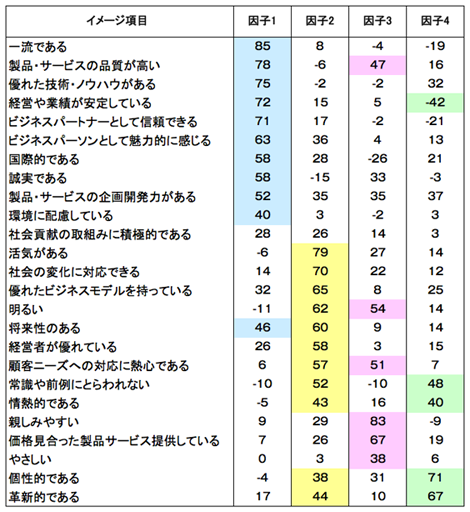
<回転とは何か>
回転は幾何学的概念である。一方、因子負荷量は解析的概念である。データ解析では、しばしば幾何学的表現と解析的表現が、同じ文脈で混在するので、慣れていないと混乱するであろう。因子負荷行列を図的に表現すれば下図のようになる。
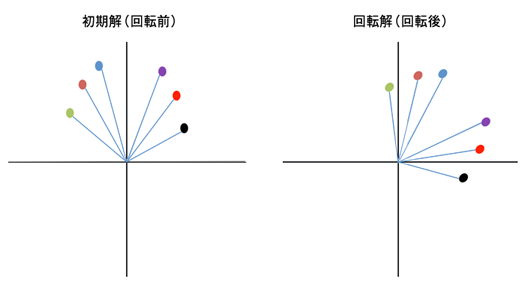
因子は2個としてあるので、因子を縦軸と横軸にすれば平面を描くことができる(3因子による空間表示でもかまわない)。変数は6個にして色分けしてある。●は因子1と因子2の因子負荷量の値を座標値とした位置にあるが、見やすいように原点からのベクトルで表現してある。これが因子負荷行列の図的表現である。
回転とは、この平面つまり座標空間で因子(軸)を「回転させる」という幾何学的イメージに準拠している。6変数の相対的位置は変わっていない。下図の回転前後は因子(軸)ではなく、変数が回転しているように見えるが、因子の方を回転しているのである。そして、この回転は360度、どのように回転することもできる。無数の回転解が存在する。因子分析は座標空間だけを定めたのである。ちなみに、これをネガティブに「因子の不定性」とか、ポジティブに「回転の自由度」などという。
<なぜ回転するのか?>
解釈しやすい解を得るためである。解釈しやすいとは、どういう状態であろうか。それは単純構造の時である。単純構造という概念はThurstoneが提案したのだが、これを解析的に実現したのがKaiserで、1958年に"The varimax criterion for analytic rotation in factor analysis"という論文としてPsychometrikaに発表した。この時、バリマックス回転が成立した。
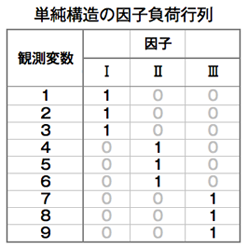
単純構造とは下図のように、ある因子には、ある変数だけが1に近い負荷量を持ち、他の変数は0に近い負荷量を持つ状態である。下図の因子Ⅰは変数1,2,3の3変数とだけ関係しているので、因子Ⅰの解釈には3変数だけを考慮し、他の6変数を無視できる。
因子負荷行列の図的表現をみると、回転前は6変数のすべてが因子1と関係している。回転後では最初の3変数は縦軸と、後の3変数は横軸と強い関係を持つように分離している。別の見方をすると、6変数が3変数ごとにグループ化された。関係の強さは幾何学的には因子の軸と各変数ベクトルとの角度の小ささである。回転後は、3変数はある因子と強く関係し、他の因子とは弱い関係になった。回転によって単純構造に接近したのである。
Kaiserは単純構造を得るには、因子負荷行列の要素の分散を(規準化したうえで)最大化すれば実現できる、というアイデアを得た。大きい負荷はより大きく、小さい負荷はより小さくなるような規準に向かって回転させるので、分散(variance)の最大化(max)、すなわちvarimaxという名前にしたのである。
最初に示した「ブランド戦略サーベイ」の初期解(回転前)は、因子1にほぼすべての変数は高い負荷を持つ。しかし、バリマックス回転後は単純構造に向かって、因子と変数とのコントラストが強化されていることが分かる。これで4因子についての解釈は容易な方向に改善されたのである。
<因子負荷量の計算>
因子分析の数理的な目標は、因子負荷量の推定である。しかし因子分析モデルは強い制約条件をもつ統計モデルである。そのため、まず計算しやすいような解を最初に求めている。それが「初期解」という名前の意味である。初期解は第1因子の分散が最大になるように計算し、次に第2因子の分散、という順番に解を求めているので、因子1の負荷量がすべて大きかったのである。
因子分析モデルの制約条件が多い理由は、因子が観測されていない潜在変数であるためである。方程式の本数よりも未知数の方が多いと、一意に解を求めることができないので制約条件を設定して計算している。回転解とはそのような制約のあとに「有用な」解を求めていくことである。なお、回転しても因子分析モデルの共通性や独自性、モデルの適合度などは変化しない。

