数量化3類
数量化3類はコレスポンデンス分析(対応分析)と数理的に同等である。 ニュートンとライプニッツによる微分の発見のように、異なる場所と時期に、同じ発見・発明がされる歴史的事例がいくつも存在する。数量化3類も、本質的に同等の分析法が、異なる開発者によって、異なる場所と時期に、異なる名前でいくつか発表された。分析結果として得られる数値は本質的に同値であり、分析結果の解釈が異なるような事態は生じない。応用事例は「コレスポンデンス分析」の項を参照されたい。ここでは数量化3類の誕生と比較を中心に解説する。
計算結果が同じになるとはいえ、開発の背景や目的、基本的な考え方、導出方法などは異なっている。
数量化3類は缶詰ラベルのデザインを創造する現場から考案された。そのため商品デザインや感性の調査・評価の分野で利用されてきた。1955(昭和30)年前後の缶詰業界は輸出による経済復興を牽引していた。デザイナーの佐藤敬之輔(1912-1979)はニチレイの缶詰ラベルのデザインの仕事をしていた。
「輸出用の缶詰ラベルに富士山や芸者がついていないと重役は承知しない。そういう人は趣味が悪いのだと示したい」
佐藤は林知己夫(1918-2002)にこのような相談をした。佐藤はさまざまなデザインを作り、いろいろな人々に、好きなデザインを選ばせた調査データを持っていた。林はこの調査データから目的を達成する解析手法を考案した。それが数量化3類であった。
昔の缶詰ラベルのデザインを集めた書籍である『缶詰ラベル博物館』の中から、芸者が使われている缶詰ラベルを図1に、富士山が使われている缶詰ラベルを図2に示す。当時のデザインの様子を伺うことができる。“フジヤマ”、“ゲイシャ”は人気があったらしい。

図1 野崎産業(現・川商フーズ)のツナ缶詰ラベル(出典:『缶詰ラベル博物館』)

図2 後藤物産缶詰(現・はごろもフーズ)のツナ缶詰ラベル(出典:『缶詰ラベル博物館』)
林も十分に変わり者だと思われる伝説が多いが、その林が佐藤のことを変わり者だと評している。佐藤は東京帝国大学では生物学を学んだが、陶芸家の内弟子になった時期もある。石油関連など多様な経歴で太平洋戦争の前後を通過した。林の家にふらり訪れて、絵を描いたり、音楽を聴いたり、泊まっていったり、ふらりと帰ったり、まるで自分の家のように振る舞っていたという。さすがの林も、この抜群のセンスの良さをもった佐藤を、変わり者だと感じていた。
林は佐藤の持ち込んだ課題をいかにして解決するか、悩んだ。ある夜、寝ようと横になったところで思いついた。人とラベルの相関係数が最大になるように、人とラベルに数量を与えれば、人とラベルをその数量で同時に並び替えたときに対角線上に集まる。趣味のよい人は趣味のよいラベルに、そうでない人はそうでないラベルに集まるパターンを構成できるだろう。この日、佐藤は泊まっていたので、朝になってから、林の思いついたパターン分析のアイデアを佐藤に話すと、それでよい・それがよいと大賛同であった。
分析結果は見事に成功した。佐藤は有頂天であったという。このようにして数量化3類が誕生した。
その後の佐藤はアフリカに興味をもった。デザインの原点を求めてアフリカに渡ったが、マラリアに罹患し帰国後まもなく亡くなった。「勝手放題、よい一生であった」と林は有能なる逸材である友人の死を惜しんだ。
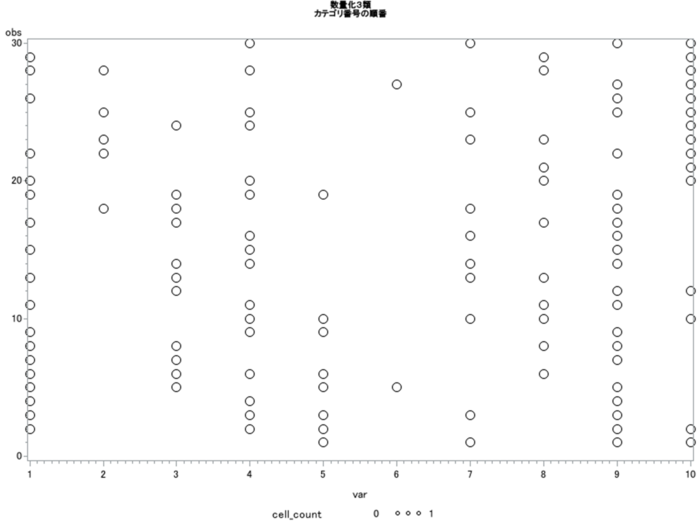
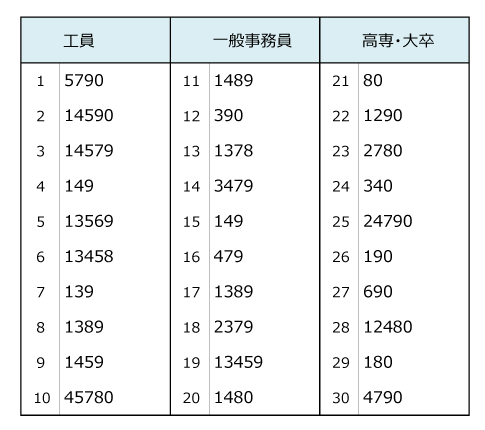
林(1956)で示された佐藤の調査データは、20歳代の30人の女性に対して、10種類の缶詰ラベル(白色を使っている、使っていない、魚類、果物類など)を提示して選好を回答した結果である。仮に30人の回答者に1~30という番号を与え、缶詰ラベルに1~10という番号を与えてみよう。この単なる連番同士の相関係数を計算してみると0.116となる。散布図を描くと図3のような様子になる。ほとんど無相関である。
そこで、回答者と缶詰ラベルの相関係数が最大になるような数量を算出すると、表1のような数量となる。この数量(スコア)を数量化法の用語では、サンプル数量、カテゴリ数量と呼ぶ習慣がある。
表1 連番と相関最大化となる数量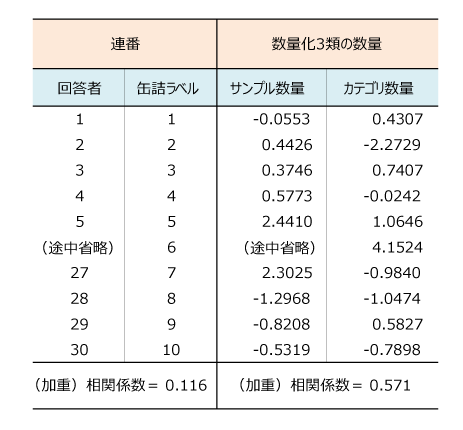
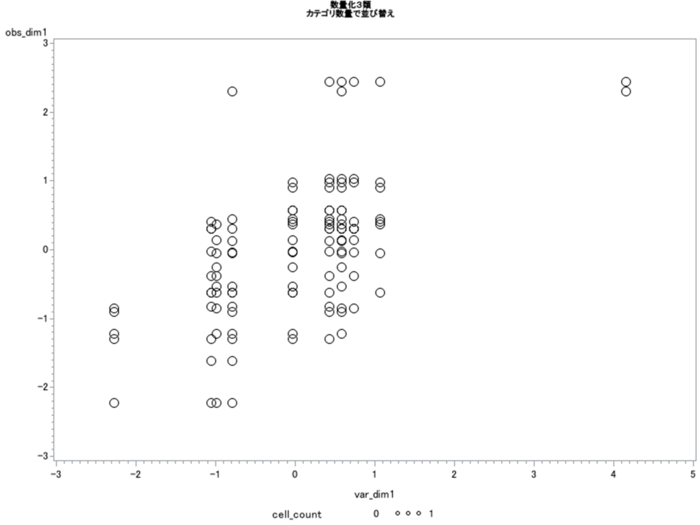
サンプル数量とカテゴリ数量で相関係数を計算してみると0.571となる。連番の相関係数0.116よりもかなり大きくなった。散布図を描くと図4のようになり、0.571に対応する程度に対角線上に集まった様子が観察できる。これが数量化3類であり、林のアイデアを解析的に実現した結果である。
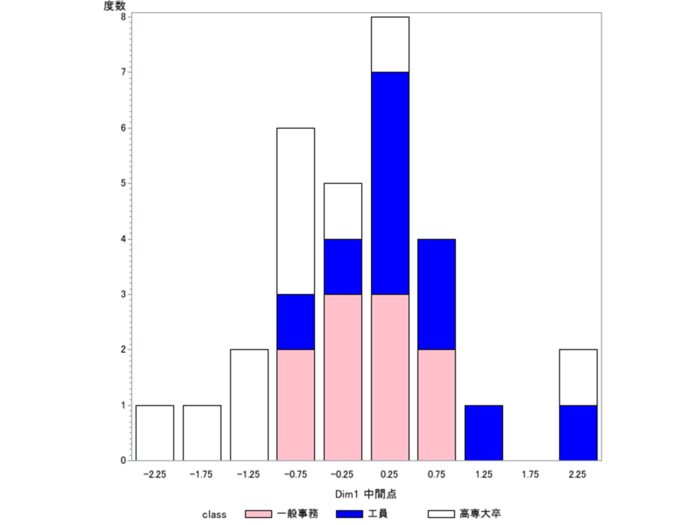
この缶詰データの回答者は、10人ずつの3グループで構成されている。「工員」「一般事務員」「高専・大卒」である。これは学歴の順序性でもある。サンプル数量の分布をヒストグラムで確認すると(図5)、3グループ別に数量の高低が比較的よくまとまった。分析にあたりグループ情報は使わずに、選好パターンだけから数量化したのだが、結果として3グループを識別する数量を得た。さらにクロス分析を検討すれば、他の背景との関連も発見できるだろう。同様にして缶詰ラベルの方も、デザインの特徴によって、グループがどのように形成されたかをカテゴリ数量から検討することができる。
<ポジショニング分析>
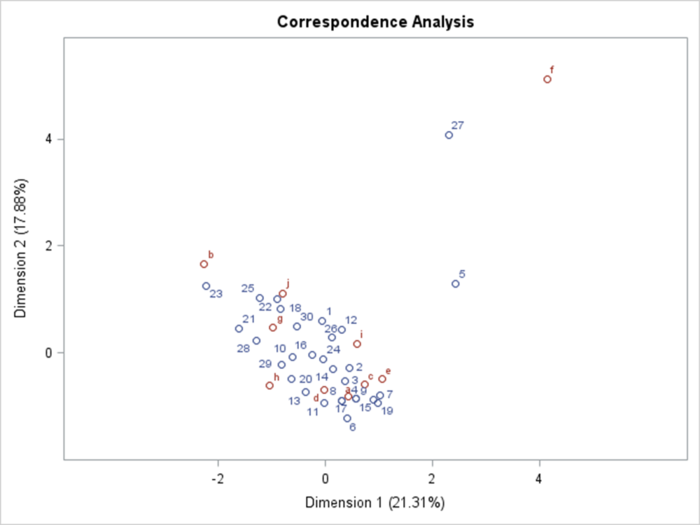
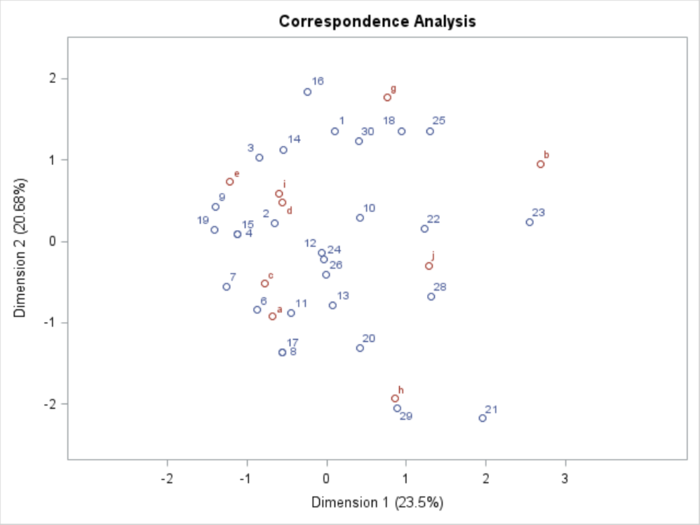
数量化3類はポジショニング分析で利用することが多い。最初の2次元を使って、回答者と缶詰ラベルの同時布置のポジショニング・マップを描くと図6のようになる。
この缶詰データは実際の調査データによくあるように「外れ値」というべき値を含んでいる。外れ値の影響を受けてポジショニング・マップが解釈しにくい結果となっている。外れ値は5番と27番の回答者、および6番の缶詰ラベル(図6では f と表記)である。このサンプル数量とカテゴリ数量は突出して異なる値となった。6番のラベルが一体どのようなデザインなのか興味深いのだが、林(1956)には具体的・個別的ラベルのデザインは掲載されていない。5番の回答者は工員であり、27番は大卒だが、それ以上の背景情報はない。すなわち、この2人だけが6番のラベルを「好き」と回答したのである。
数量化3類をポジショニング分析で利用する場合は、外れ値の扱いに苦慮する場合もある。外れ値の対処方法は、数学的問題である以前に現実的・具体的問題であり、一般的な解決法が存在しないが、少なくとも原因を追究することから始める。単純なエラーではないということが確認できた場合は、データの背景をよく理解したうえで再度分析をする。この場合、「2人の変わり者と1個の変わりラベル」という特殊なケースがあるという認識をしたうえで、これを除外してポジショニング・マップを検討する余地がある。外れ値を除外すると、図7のように著しく印象が異なるマップになる。
センスのよいデータサイエンティストであれば、ここで考えるだろう。外れ値を除外したら、図4の相関散布図の様相も変わり、最大化された相関係数は0.571より、著しく悪化するのではないだろうか--と。自身で確認されたい。
<コレスポンデンス分析との関係>
数量化3類とコレスポンデンス分析(対応分析)は、数理的には本質的に同値であることを、具体的な分析結果の数値を使いながら確認しよう。数式による証明は専門書に書かれている。なお、以下の説明でも特異値分解、固有値分解などの用語が出てくるが、詳細は線形代数の知識が必要なので解説をしない。これは計算方法に過ぎないし、実際はソフトウエアが計算してくれるので、ユーザーは分析結果の意味を理解していれば調査データの分析ツールとして利用できる。クルマの内部機構を知らなくてもクルマを運転できるという状況と似ている。
表2に数量化3類(以下、3類と略す)とコレスポンデンス分析(以下、CAと略す)の座標値を示した。それぞれの用語の習慣に従い、CAでは行座標と列座標とした。3類のサンプル数量とカテゴリ数量に対応する。3類とCAの数値が異なることは一目瞭然である。表の下行に平均と分散を計算してある。平均はいずれも0である。単位のない尺度の平均を0に置くことは自然な数学的処理である。3類の分散は1だが、CAは0.326となっていて異なる。つまり基準化の方法が異なっている。そして、それが違うだけである。
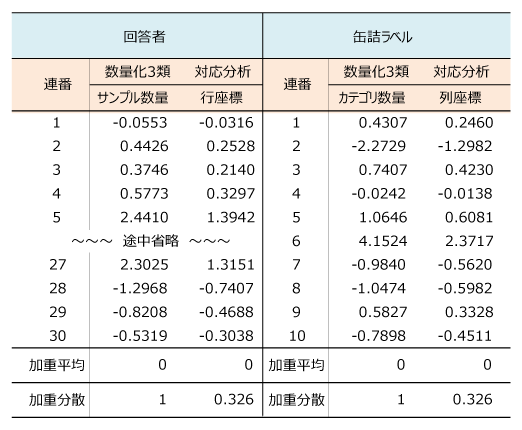
3類の数量でCAの座標値を割ってみよう。最初の2人の回答者では、
0.2528 ÷ 0.4426 = 0.571
同様に、最初と最後の缶詰ラベルでは、
-0.4511 ÷ -0.7898 = 0.571
となっている。つまり3類とCAは定数倍の比例関係にある。従って、3類とCAの相関係数は正確に1である。その意味で本質的に同値なのである。ポジショニング・マップを描いても同じパターンが描かれる。
(平均、分散、相関係数はいずれも周辺度数で加重した平均、分散、相関係数である)
3類の数量に定数0.571を乗じた値がCAの座標値であることを確認した。この定数0.571は何かといえば、このデータが達成し得る最大の相関係数0.571なのである。林が3類で最大化した相関係数である。
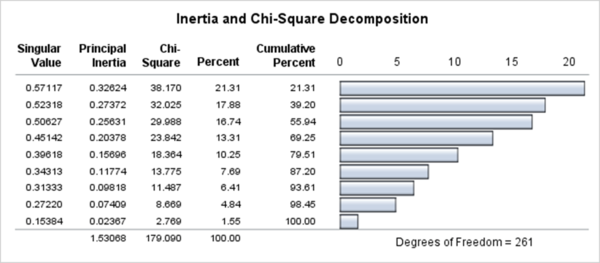
ところでCAを実行するソフトウエアが最初に出力する結果は、一般に図8のような形式をしている。CAは頻度行列の特異値分解をしているので、その報告をしているのである。図8はSASのCorrespプロシジャの出力結果である。見慣れない表でもあり、何が報告されているのか解説をする。
最初の列に特異値(Singular Value)が表示されている。第1特異値が0.571であることが分かる。じつは、この特異値は3類が最大化した相関係数0.571そのものである。
第2列に主慣性(Principal Inertia)が表示されている。第1主慣性が0.326であることが分かる。これが表2におけるCAの座標値の分散0.326である。主慣性は特異値の二乗である(0.57117 ** 2 = 0.32624)。固有値分解における固有値に相当する。主成分分析との類比で述べると、主成分スコアの分散が固有値で基準化されたように、座標値の分散を主慣性で基準化しているのである。
( 慣性 Inertia と呼ばずに、分散でもよいのだが、CAの最初の提唱者の命名に従う習慣である。産みの親には命名権がある。慣性のほかに質量などもあり、CAでは統計量に物理学の概念・名前が使われている。)
一方、特異値が相関係数(とくに正準相関係数という)であったが、それなら主慣性は相関係数の二乗ということになり、それは決定係数(R2乗)ではないかということになる。実際、そうである。決定係数は全変動の説明割合であった。ここでは第1主慣性は21.31%であると寄与率として示されている(0.32624÷1.53068 = 0.2131)。3類では数量の分散を1とするが、これは主成分分析においても、主成分の分散を固有値ではなく1に基準化することがある事情と同様である。その時は、主成分分析ではなく因子分析(主成分解)と呼ばれることがある。CAは分散1ではなく特異値を乗じているが、この意味は点間距離をカイ二乗距離の近似として解釈できるという統計理論的な整合性にある。林は統計量の意味よりも、パターンを発見できれば座標の寸法はどうでもよい、と考えたので3類の数量の分散を1としたのである。3類とCAの計算上の違いは、特異ベクトルに特異値をかけるか否か、である。
第3列にはカイ二乗値(Chi-Square)が表示されている。CAが頻度行列のカイ二乗値を分解することを目標としているからである。これは、表を標準化しているという程の意味であり、多変量データ行列において変数を平均0、分散1などで標準化することに相当する。缶詰データを頻度行列(クロス表)とみなしてカイ二乗値を計算すると179.090となる。これが下行の合計179.090である。カイ二乗値は主慣性の117倍である(0.32624×117=38.170)。117とは総度数である。缶詰データを「回答者×缶詰ラベル」30×10の行列として表現する。「好き」との回答を1とし、それ以外を0とすると、30×10の二値データ(0-1反応)行列となる。全部で300のセルのうち1(好き)のセルが117なのである。これが総度数である。
注意すべき理論的問題はある。CAの行座標の分散と、列座標の分散が同じ値0.326であったことから示唆されているが、CAは行と列を同等に扱っているのである。多変量データ行列においては、行である回答者と列である変数は別個に扱い、標準化は変数に対して実施する。それがCAでは行と列を同等に扱っている。これが何を意味しているかというと、解釈は行と列で個別にしなければならない、ということである。解釈とは点間距離(カイ二乗距離)の遠近の解釈である。回答者の間の距離を解釈してよいし、缶詰ラベルの間の距離を解釈してもよい。しかし、ある回答者とある缶詰ラベルの距離は、数学的には定義されない、という問題がある、ということである。これは3類において分散を1に基準化しても同じである。この問題があるため、行要素と列要素の同時布置図の作成をすべきでない、という理論的(?)立場もある。出力しないソフトウエアもある。しかし同時布置は便利であるし、それを解釈したい誘惑を避けられないだろう。特に3類の開発の発想はそこにこそあったとさえいえる。
点間距離ではなく、座標上の方向性を解釈することであれば、間違いを起こさない。そのような場面では、数学的厳密さでカイ二乗距離を比較しない。そのような態度で解釈するほうが不自然である。缶詰ラベルのデザインの選好である。「AよりBのデザインが3ミリ好きです」というような測定はしていない(できない)のだから、結果の解釈もその程度の曖昧さを考慮して<数値>を扱うセンスが必要である。感性という現象を、できるだけ客観的にデータの情報から数量化した、という分析であって、身長や体重のような物理量の測定ではない、ということも忘れないで解釈するのである。厳密に正しく計算する、ということと、分析結果の数値から厳密に1ミリ単位で感性の差異を議論する、ということは次元が違う。またいい加減に調査してもよい、ということでもない。林は数理的手法の開発だけでなく、このような、複雑あいまいな社会現象や心的状態の分析態度についても述べてきた。質的な情報を量的な数量に転換する、ということを深く考えた研究者であった。
結局、3類はパターンを発見する狙いで、相関を最大化する目的関数を定義して最適化計算をした。CAは頻度行列に対して線形代数の特異値分解による定式化をしたのだが、それが数学的には同じ解に帰着していた。3類は日本で林によって独立に開発されたが、国際的には1930年代から複数の類似手法が発表されている。世間の解説の中には、クロス集計表を分析するのがCAで、0-1の反応行列を分析するのが3類であるという説明もみかけるが、間違いである。そこに違いがあるのではない。
<参考>
林(1956)に掲載されている原データは表3のとおりである。各列に10人の回答値があり、10人×3列=30人のデータである。各列は「工員」「一般事務員」「高専・大卒」の3グループでもある。各行の数字は缶詰ラベルの種類(1~9,0)を表現している。
線形代数によるコレスポンデンス分析の表現は以下のようになる。表3の原データを2値(0-1)に変換した30×10の行列を作成したうえで、各セルを総度数で除した行列をPとする。Pの一般化特異値分解、
で得た左右の一般化特異ベクトルAとBから、行座標Fと列座標Gの基準化を、
G = DC-1BDu
とする。これがコレスポンデンス分析の行座標と列座標である。数量化3類では基準化方法が異なり、以下のように定義する。
G = DC-1B
これがサンプル数量Fとカテゴリ数量Gである。
ここで Duは一般化特異値を対角要素とする対角行列である。 DRと DC は P のそれぞれ行和、列和を対角要素とする対角行列である。
30人の回答者が「好き」と答えたラベル(1~9, 0)
<文献>
林知己夫(1956)数量化理論とその応用(II).統計数理研究所彙報.4(2), 19-30.
※ 統計数理研究所のWEBサイトからPDFファイルを取得できる(URL)
日本缶詰協会(2002)缶詰ラベル博物館.東方出版.