数量化1類
数量化1類は予測を主目的とするデータ解析の手法である。市場調査の分野では1960年代以降、新聞広告の注目率調査データに適用されてきた。特に林・村山(1964)『市場調査の計画と実際』(日刊工業新聞社)の中で、広告注目率の調査データに対して、数量化1類を適用して予測分析する事例が紹介されたことが大きな影響を与えた。これは数量化法を解説した最初の出版であった。現在でも新聞社や広告代理店が参加しているJ-MONITOR(新聞広告共通調査プラットフォーム)の広告接触率調査で数量化1類が利用されている。
多数の新聞広告について読者調査を実施して注目率を作成し、これを目的変数(従属変数)とする。説明変数(独立変数)は新聞広告の属性である。広告の注目に影響がありそうな属性として、たとえば以下のような項目を説明変数として選ぶ。説明変数を数量化1類の用語ではアイテムと呼ぶ。どのアイテムの予測力が大きいのかを分析・解釈することも目的であり、その場合はアイテムを要因と呼ぶことがある。これを要因分析という。
数量化1類が分析対象とするデータの特徴は、アイテムの値が量的ではなく質的だという点にある。数量化法が質的データの解析手法だと説明されるのはこのためである。上記の例では、広告内容と掲載面は名義尺度、広告段数は順序尺度である。アイテムの値を数量化1類ではカテゴリと呼ぶ。
数量化1類の数理的な目標は、目的変数(広告注目率)を、もっともよく予測できるようにカテゴリに数量を与えることである。これをカテゴリ数量と呼ぶ。質的なカテゴリに数量を与える手法であることから、数量化法という名称がつけられた。
<分析例>
選挙予測では立候補者の得票率を事前に予測することが目的である。事前の標本調査(選挙予測調査)で得られる調査支持率と、選挙結果の得票率は一致するわけではない。そこで選挙区や立候補者の属性をアイテムとして説明変数に加えて、調査支持率を選挙結果の得票率によりよく近づけるようにデータ解析を実施する。このようにして構成した予測モデルを、次回の選挙前の事前調査データに当てはめて得票率を予測するのである。
2016年参院選・選挙区選挙における一人区の立候補者の得票率を、政党・職歴・性別の3つのアイテムを使い、数量化1類で分析した結果を示す。決定係数は0.446であった。
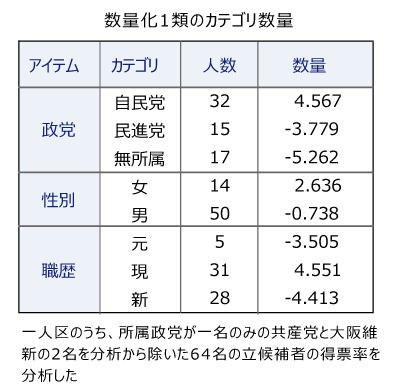
カテゴリ数量は棒グラフで視覚化すると解釈が容易である。アイテムが予測に与える影響力はカテゴリ数量のレンジ(カテゴリ数量の最大値と最小値の差=範囲)の大きさで判断する。
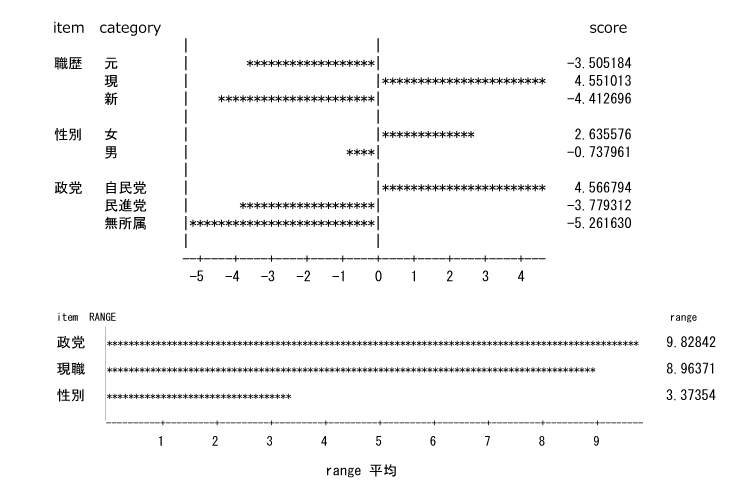
カテゴリ数量は棒グラフで視覚化すると解釈が容易である。アイテムが予測に与える影響力はカテゴリ数量のレンジ(カテゴリ数量の最大値と最小値の差=範囲)の大きさで判断する。
予測に与える要因としては政党がもっとも強く、カテゴリ数量を確認すると自民党が高い。次に職歴の予測力が高く、カテゴリ数量をみると現職が有利であると解釈できる。性別は予測力が弱いが、男性よりも女性が高めになっていると判断できる。このようにアイテムの解釈をすることを要因分析と呼んでいる。
<分散分析との比較>
数量化1類と同じデータ形式を分析対象とし、数理的に同値の結果を得る手法として、よく知られている分散分析がある。数量化1類におけるアイテムとカテゴリを、分散分析では要因または因子(factor)と水準(level)と呼んでいる。
数量化1類を理解する目的で、分散分析と比較する。以下に分散分析の典型的な事例を示す(岩崎, 2006)。ある化学物質の収量を目的変数とし、説明変数(因子)として触媒(因子A)と温度(因子B)を考えて実験を計画しデータを集める。この2因子の影響を評価するのが分散分析の目的である。因子の水準はAとBともに3水準(高・中・低)である。これは2因子実験なので二元配置の分散分析という。また同じ因子・水準の組み合わせのもとで複数回の測定する場合は特に「繰り返しあり」という。
このデータを分析した結果の決定係数は0.648であった。
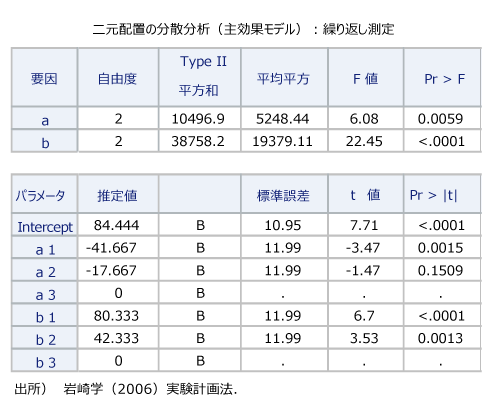
分散分析表とパラメータの推定値が出力されているが、数量化1類のカテゴリ数量は、この推定値と同値である。また、分散分析表と推定値の表は、重回帰分析の出力形式とまったく同じである。つまり、数量化1類、分散分析、重回帰分析は名前こそ違うが、数理的には同等である。数量化1類と分散分析は、アイテム(因子)のカテゴリ(水準)をダミー変数(二値変数)に変換したデータの重回帰分析である。カテゴリ数量とは、回帰係数(推定値)なのである。
<分散分析との違い>
数理的に同じだが、相違点を認識していることも、データ解析・解釈をするうえで役に立つ。分散分析は1920年代の英国でフィッシャーが開発し、数量化1類は1950年代の日本で林知己夫が開発した。分散分析は既に存在していたが、数量化1類は独立に導出された。
適用分野の背景が異なる。フィッシャーは農場において農作物の育成の条件を最適化する研究をするなかで実験計画法と分散分析を考案した。林はGHQの占領政策として、日本語の漢字廃止・ローマ字化をする方針の是非を検討するために、日本人に対して実施した標本調査データを分析するために数量化1類を考えた。この調査は「日本人の読み書き能力調査(Literacy Survey)」(1948年)という。フィッシャーは自然科学的な、林は社会科学的な背景を背負っていた。
データの性質が異なる。実験計画法によるデータは要因を統制してデータを収集する(実験する)ので、要因間が無相関になるようにバランスを考慮して実験が計画される。標本調査法によるデータは母集団から無作為抽出はしているが、アイテム間を統制した実験はできない。具体的には、学歴や年収の水準の異なる世帯集団を無作為に作って(統制して)、そこで生まれ育った子供が18歳になった段階で調査を実施し、学力成績と環境要因との因果関係を分散分析で検証する、というような社会実験は現実的に不可能だということである。
このようなデータの性質の相違がもたらす重要な結果は、要因別の影響力を比較するに当たり、実験計画法のデータでは決定係数を要因ごとの寄与率に分解して解釈できるのに、標本調査法のデータではそれが数理的にできない――という相違となってあらわれる。
以下に示すように、数量化1類では政党・職歴・性別の各アイテム単独の寄与率の合計(0.693)は、3アイテムによるモデルの決定係数(0.446)と一致しない。アイテム間に相関があるため情報に冗長性が生じているのである。この問題は重回帰分析の用語で多重共線性と呼ばれている。一方、実験計画法で収集したデータの分散分析では決定係数(0.648)を要因ごとの寄与率に正確に分解して「温度の影響力は51%である」のように解釈が容易にできる。数量化1類では「政党の影響力は35%である」というような解釈が数学的にできない。
数量化1類:決定係数(0.446)≠政党+職歴+性別( 0.354 + 0.333 + 0.007 )=0.693
分散分析:決定係数(0.648)=触媒+温度( 0.138 + 0.510 )=0.648
要因分析の方法が異なる。数量化1類ではレンジが大きいアイテムの影響力が強い、と記述的に解釈する。分散分析では統計的検定によって推測的に判定する。調査データのサイズは実験データよりも大規模なので、検定結果が有意になりやすいという事情もある。参院選の得票率データに関しても分散分析を適用することは可能であり、以下のような結果を得る。性別のF検定の結果(P値=0.2409)は有意ではない、つまり得票率の予測に効果がない、という判定をするのが分散分析の手順である。
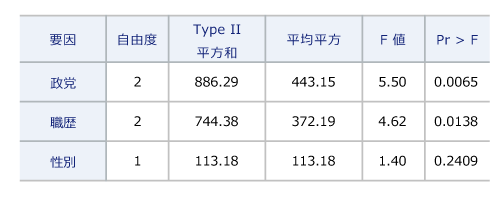
以上のような相違もあって、数量化1類は市場調査・世論調査・社会調査の分野で、広告注目率や選挙予測など質的変数から予測する場面で利用されてきた。分散分析は農業のほか、食品業の官能検査、製造業の品質管理や、製薬業における薬効など実験可能な分野で利用されてきた。
ちなみに、市場調査でもコンジョイント分析が製品開発のために利用されている。コンジョイント分析は数理的には分散分析であり、データ収集法でも実験計画法を使う。
最近になって、調査・統計に関する雑誌において、下記のような数量化法に関する特集が編集された。多様な視点からの議論がされている。
「特集 数量化理論の現在」『社会と調査』No.9(2012年9月).社会調査協会.
「特集 林知己夫生誕百年記念」『行動計量学』45,2(2018年9月)日本行動計量学会.

