信頼区間
信頼区間(confidence interval)とは、調査結果の精度を知るための統計科学的な推測法である。統計的推定あるいは区間推定という。信頼区間をどのように使うのかを<例1>に示す。
<例1>
自社の商品Aは、日本に在住している一般消費者(15歳以上の男女・国籍を問わない個人)を対象として販売している。現在の利用率(%)を知りたいので千人を対象に標本調査を実施したところ35%が「利用している」との回答結果であった。
15歳以上の人口は、外国籍の日本在住者も含めて1億1114万9千人(2015年10月1日現在)である。調査したのは千人のみであるから、この調査結果には全員を調査していないことによる標本誤差がある。そこで誤差幅(誤差の大きさ=精度)を計算したところ、3%であった。これが信頼区間であり、以下のように表現する。
[ 32%, 38% ]
すなわち32%~38%の範囲の誤差を伴う。調査結果の35%という数字は母集団における真の利用率(1億1千万人強の全員を調査した結果)と一致していない可能性がある。それでは調査結果の「35%」はどの程度の精度か、という統計科学的な評価方法として利用する。「35%」は点推定といい、「32%~38%」を区間推定という。
<比率の信頼区間の計算方法>
比率の信頼区間 $C_\pi $の計算は、以下の公式で求めることができる。
\begin{align} C_\pi & = \left[ p-z_{\alpha/2} \frac{ \sqrt{p(1-p)} }{ \sqrt{n} } , p+z_{\alpha/2} \frac{ \sqrt{p(1-p)} }{ \sqrt{n} } \right] \tag{1} \\ & =\left[ 0.35-1.96 \frac{ \sqrt{0.35(1-0.35)} }{ \sqrt{1000} } , 0.35+1.96 \frac{ \sqrt{0.35(1-0.35)} }{ \sqrt{1000} } \right] \tag{2} \\ & =\left[ 0.35-0.0296 , 0.35+0.0296 \right] \tag{3} \\ & =\left[ 32\% , 38\% \right] \tag{4} \end{align}
これは比率・割合(%)の信頼区間を求める式であり、利用率だけでなく内閣支持率など、調査結果で得るさまざまな「割合」の精度を計算するために使う。この公式は数理統計学が理論的に導出しているが、直観的には以下のように理解できる。
「私達は一回しか調査を実施しないので、実践的には一つの利用率しか入手できない。しかし理論的には標本サイズ $n$ のすべての可能な標本の調査結果(利用率)を想定可能である。すべての可能な利用率の標本分布を知っているのなら、手元にある一つの利用率の精度を推定する手段があるだろう」
- (1)式に出現している記号は以下のとおりである。
$p$ :標本比率(例1では利用率)
$n$ :標本サイズ(例1では千人)
$z$ :標準正規確率変数
$\alpha$ :正規分布の両側確率
$\alpha$ については注意が必要である。正規分布(確率分布)の両側「確率」ではあるのだが、推定の文脈では $\alpha$ を確率と呼ばない。$(1-\alpha)$ には呼称があり、信頼係数、信頼率、信頼度などという。信頼率や信頼度という用語は、別の分野で異なる意味で使われるので、誤解を避ける必要がある場合は信頼係数を使う。ちなみに、検定においては $\alpha$ の方に呼称があり、危険率、有意水準、第一種過誤などという。
推定: 信頼係数・信頼率・信頼度 $(1-\alpha)$
検定: 有意水準・危険率・第一種過誤 $(\alpha)$
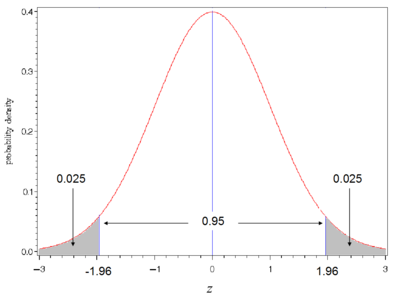
$\alpha = 0.05$ に設定することが多いが、この設定は任意である。$\alpha = 0.05$ の場合、 $z_{\alpha/2}$ とは上側確率が0.025となる標準正規確率変数 $z$ の値であり、 $z_{\alpha/2}=1.960$ である。信頼係数は百倍して%で表示することも多く、その場合は標準正規確率変数の値も%点として表現する。$\alpha = 0.05$ であれば信頼係数 $(1 - \alpha)$ は95%であり、上側2.5%点は1.960である。その信頼区間は「95%信頼区間」という。例1の計算結果である「±3%」は95%信頼区間である。
信頼係数は90%でも99%でも、目的に応じて任意に設定できる。信頼係数99%(上側0.5%点)と信頼係数90%(上側5%点)の信頼区間はそれぞれ以下のようになる。
- 信頼係数 $99\% ( z = 2.580) \pm4\% $
- 信頼係数 $95\% ( z = 1.960) \pm3\% $
- 信頼係数 $90\% ( z = 1.645) \pm2\% $
<前提条件>
信頼区間の計算は(1)式に標本サイズ $n$ と標本比率 $p$ を代入するだけだが、計算結果を使えるための、いくつかの前提条件がある。もっとも重要な前提は、
「標本が母集団からの確率標本である」
ということである。
例1の場合、目標母集団は「日本に在住している一般消費者(15歳以上の男女・国籍を問わない個人)」である。枠母集団として住民基本台帳を使用した無作為抽出が、この前提を満たす具体的な手順の一つである。
例1の公式は単純無作為抽出を前提としている。実際の標本調査においては測定方法に応じた抽出方法が適用されるが、確率抽出であることが本質的に重要である。複雑な抽出方法であれば信頼区間の計算公式も複雑になるが、単純無作為抽出の公式で代用することが多い。
確率標本でない場合、信頼区間の計算は形式的にはできるが、その計算結果は理論的には無意味である。たとえば以下のような例である。いずれも標本抽出方法に依存しており、測定方法に起因する問題ではない。
<インターネット調査>
インターネット調査は調査機関によるパネル・モニター方式による実施が多い。実際のモニター人数は多くても数百万人である。仮に1千万人だとしても、母集団の一割にも満たない「応募者集団」に偏っている。モニターを枠母集団とした無作為抽出であっても、信頼区間は1千万人のモニター集団を推測しているのである。科学的な標本調査は1億人強の目標母集団を推測するのであって、インターネット調査のような小さな母集団ではない。
測定法としてのインターネット調査が問題なのではない。たとえば架空の想定であるが、住民基本台帳から適切に無作為抽出した調査対象者に、インターネットでWEB調査を実施できれば、理論的な前提条件は満たされる。しかし今のところ、実践的条件が整わず実現できないだろうが。
目標母集団の定義が「ある新製品発売1月以内の購入者」であれば、モニターから迅速にこの稀有な該当者を集められることがあり、インターネット調査は優れた手法となる。
<割当標本>
性別・年齢別・地域別などの分布を、国勢調査に合わせてセルの人数を決めておき、調査に協力してくれた人から順に対象者として割り当てる方法を割当法という。これは非確率標本であり、信頼区間によって目標母集団を推定する理論的根拠がない。インターネット調査、郵送調査、調査員調査など測定法とは直接関係ない。
無作為抽出法のような「計画標本」という概念がないため回収率を定義できないが、訪問調査員が依頼人数を記録しておき、快く調査に協力してくれた人が、全体として20人に1人だったら、回収率は5%である。このわずか5%の「親切な集団」は調査目的によっては、きわめて偏った特殊な集団になっている可能性がある。
他に以下のような理論的な前提条件があるが、上記の前提(確率標本であること)よりも深刻ではない。市場調査・社会調査・世論調査ではほとんどの場合に大標本を扱うからである。
(前提1)二項分布の正規近似
割合の標本分布は理論的には二項分布から導出されるが、例1は正規分布を使っている。標本サイズが大きければ正規近似できる。正規分布は二項分布の $n \rightarrow \infty$ のときの極限分布である。
(前提2)母集団分布の正規性
母集団が正規分布でない場合。これも標本サイズが大きくなれば、母集団がどのような分布であっても、標本平均や標本比率は正規分布に漸近する。これを中心極限定理という。
(前提3)母分散未知
母集団の分散が未知の場合。これも標本サイズが大きければ、母集団分布が非正規であっても、標本不偏分散を母分散推定値として適用できる。
<標本誤差と非標本誤差>
信頼区間の推定は、標本誤差に関する議論である。非標本誤差については考慮されていない。代表的な非標本誤差は無回答誤差(調査不能誤差)である。
たとえば例1の回収標本サイズは千人であったが、計画標本は二千人だったと想定しよう。つまり回収率が50%だったのである。この商品は利用者の好き嫌いが激しくて、調査対象者のうち、他社ユーザーは調査に協力してくれなかったと仮定しよう。つまり回収できなかった半数の千人は利用者でなかったのである。
計画標本である二千人を無作為抽出する手順は統計科学的に適切に実行されたとして、この仮定の状況では、本当の利用率は35%ではなく、実は18%に過ぎない。
この非標本誤差の大きさは、信頼区間の±3%のような標本誤差よりも桁違いに大きく、もはや標本誤差の検討など無意味になる。標本調査において回収率を重視する理由はここにある。回収群と非回収群が異質の場合、低すぎる回収率は深刻な問題である。
<信頼区間の理解と誤解>
95%信頼区間を以下のように誤解しやすい。
「母集団における真の利用率(母比率)が35%±3%の範囲に存在する確率は95%である」
この解釈は間違いである。調査結果の35%±3%に真の値が存在する確率は1か0であり、その中間ではない。母数は定数であって確率変数ではない。確率的に分布するのは標本である。信頼区間が確率的に分布するのである。信頼区間とは以下のように理解する。
「繰り返し無作為抽出を実行し、そのたびに信頼区間を構成すると、そのうちの約95%の信頼区間が母比率を含む」
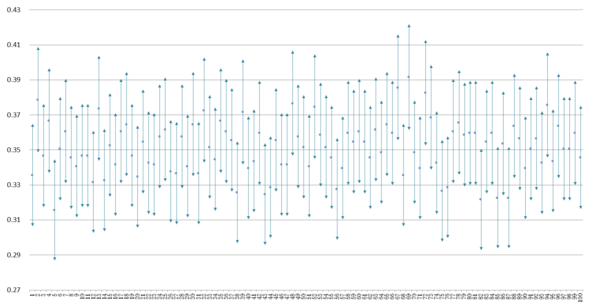
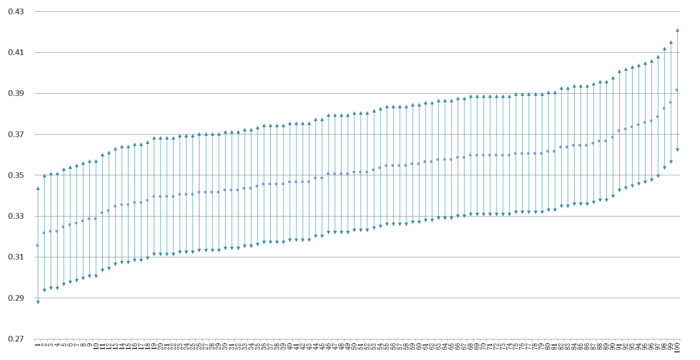
この表明に納得感がないとしたら、恐らくその理由は、私たちは調査を一回しか実施しないから、手元に一つの利用率しかないからである。そこで全知全能の神の立場にたって、母集団における真の利用率を知っていると仮定しよう。そのうえで母集団からの無作為抽出標本の信頼区間がどのように分布するか確認しよう。これはコンピュータ・シミュレーションによって可能であり可視化できる。真の利用率が35%である母集団から無作為抽出を100回実施して、それぞれの標本における100本の95%信頼区間を構成した。その結果をまとめてグラフで示したのが下図である。
見易さのために信頼区間を点推定値の小さい順から並べ替えると、35%の真値を含まない信頼区間が4つあることが見つけられる。これが95%の信頼率という意味である。私たちの一回だけの調査がどれかは未知だが、運悪く両端の標本を抽出してしまう危険度は5%だと考えて調査結果を利用するのである。
母集団からの標本統計量がどのように分布するかという性質を、上記のようにシミュレーションによって可視化したことを、数理統計学や確率論は理論的(数学的)に明らかにしている。
標本比率 $P$ は母比率 $\pi$ を中心に正規分布し、標準誤差の1.96倍の左右範囲に含まれる確率が95%であると(5)式は述べている。 \[ Pr\left( \pi - 1.96 \sqrt{\frac{\pi(1-\pi )}{n}} < P < \pi + 1.96 \sqrt{\frac{\pi(1-\pi )}{n}} \right) = 95\% \tag{5} \] (5)式を母比率 $\pi$ について解くことができ、(6)を得る。 \[ Pr\left( P - 1.96 \sqrt{\frac{\pi(1-\pi )}{n}} < \pi < P + 1.96 \sqrt{\frac{\pi(1-\pi )}{n}} \right) = 95\% \tag{6} \] (6)式は、しばしば(7)式のように書く。 \[ \pi=P \pm 1.96\sqrt{\frac{\pi ( 1- \pi )}{n} } \tag{7} \] (6)式と(7)式は、母比率 $\pi$ が標本比率 $P$ の左右の区間に95%の確率で存在する、と述べているように見えるが、(5)式から(6)式で $P$ と $\pi$ が「転倒」した際に、その役割も一緒に「変更」されたわけではない。母比率 $\pi$ は定数のままであって確率変数に「変化」したわけではない。 従って、定数である母数 $\pi$ に関する確率は議論できない。確率変数は依然として、標本比率 $P$ のほうであり、また信頼区間のほうである。
(5)式は母集団から標本に向かって演繹的に確率分布の性質を述べている。母集団は既知であり、すべての可能な標本の分布を定式化する確率論である。(6)式は逆に、標本から母集団に向かって帰納的に推測している。母集団は未知であり、手元のひとつの既知の標本から未知の母集団への統計的推測である。 (7)式には母比率 $\pi$ があるが、もちろん$\pi$は未知である。(前提3)により、$\pi$ を $p$で置き換えると、(8)式のようになる。 \[ \pi=p \pm 1.96\sqrt{\frac{p ( 1- p )}{n} } \tag{8} \]
標本比率 $P$ は調査を実施してデータを得たあとは確率変数ではなく、確率変数 $P$ の実現値 $p$ となる。(8)式に調査結果の標本比率 $p = 0.35$ を代入し、信頼区間を計算したら、その区間に母比率 $\pi$ が含まれている確率は1か0(含まれているか否か)であって、その中間ではない。95%は確率ではないから確率とは呼ばず、信頼率と呼ぶ。100回中95回の頻度で信頼できるだろうと考える。
$\pi$ と $P$ と $p$ を使い分けており、理論的に過ぎるようだが、以上のような信頼区間はネイマンによる研究成果で、このような考え方を頻度論という。既に同時代のフィッシャーがネイマンの信頼区間を批判(ほぼ喧嘩)したが、ネイマンの論理は数学的には完全であり、ネイマン流(あるいはネイマン-ピアソン流)の統計学が世界的主流(世界中の大学で教えられ、研究法に採用)となり、その意味で「伝統的な統計学」とも呼ばれる。
一方、母比率を定数ではなく確率的に変動する変数として扱うという発想は、本当は自然な発想であるかも知れない。ベイズ統計学がその立場である。今後の統計学の流れが変わる可能性もある。
<簡単な公式>
比率の信頼区間の公式を変形して簡単にしよう。それには信頼区間の項を、1.96は2とし、$\pi(1-\pi)$ は最大値となる $\pi=0.5$ とする。これによって信頼区間は狭い方向に推定することは無く、その意味で誤差を安全に見積もることができる。その結果として得る(11)式は簡単なので覚えておくことができる。 \begin{align} \pi &= p \pm 1.96 \sqrt{\frac{\pi(1-\pi)}{n}}\tag{9} \\ \pi &= p \pm 2 \sqrt{\frac{0.5(1-0.5)}{n}}\tag{10} \\ &= p \pm \frac{1}{\sqrt{n}} \tag{11} \end{align}
<例2>
上場企業の売上高の平均値を標本調査で調べる。2017年時点の決算データをそろえた3532社の売上高を母集団とし、300社を単純無作為抽出(復元抽出)して売上高の平均値と信頼区間を算出する。上場企業の売上高は公表されているので全上場企業(ここでは3532社)の売上高の母平均と母分散は既知であるが、それを知らないと仮定して300社の標本調査を実施したところ、平均は3126億5664万円で、標準誤差 $\sqrt{\frac{s^2}{n}}$ は719億4539万円であった。
<平均値の信頼区間の計算方法>
平均値の95%信頼区間は、比率の信頼区間と同様に、大標本を前提として以下の公式で求めることができる。 \[ \mu=\overline{x} \pm 1.96\sqrt{\frac{s^2}{n} } \tag{12} \] $\mu$ :母平均
$\overline{x}$:標本平均(観測後)
$s^2$:標本不偏分散
$n$:標本サイズ(例2では300)
従って、95%信頼区間は、以下のとおりである。
3126億5664万円 ±1410億1296万円
<母集団の平均値>
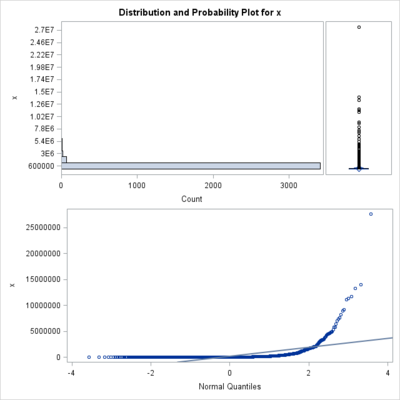
平均が3126億円で、誤差の幅が±1410億円であるが、印象的には大きな誤差幅である。上場企業の売上高は実際には分かっている。母平均は1979億3480万円である。300社の標本調査の平均値は3000億円超であり大きな差であるが、95%信頼区間には収まっている。 売上高や世帯所得のような社会現象の変数の分布は、身長のような自然現象の変数とは異なって正規分布はせずに、偏った分布をすることがある。トヨタ自動車の27兆5971億円から、アドメテックの400万円まで分布している。下図のヒストグラムのように指数分布の形になっている。これが、誤差幅が大きくなる背景である。バラツキが大きければ信頼区間も拡大する。(12)式の分子にある$s^2$はそのことを述べている。
<例2>を確認した関連で、二つの疑問が生じる。
● 著しく偏った分布の母集団から単純無作為抽出法を適用してよいのか?
● 標本が正規分布に漸近する(前提2)はこんな母集団でも成り立つか?
<企業の抽出方法>
企業を母集団とする標本調査の場合は層化抽出が適用されることが多い。単純無作為抽出よりも精度が高まる。総務省の「サービス産業動向調査」では業種と規模で層化抽出し、資本金1億円以上の層は悉皆層として全数調査をする。
例2ではトヨタ自動車が抽出されるか否かで大きな影響を受けることは自明であり、少数の巨大企業は必ず調査対象とするのである。有権者個人を対象とする世論調査では一人ひとりの重みは等しいが、企業は違うので等確率ではない確率で抽出する。分散が大きい層の標本は高い確率で抽出する。
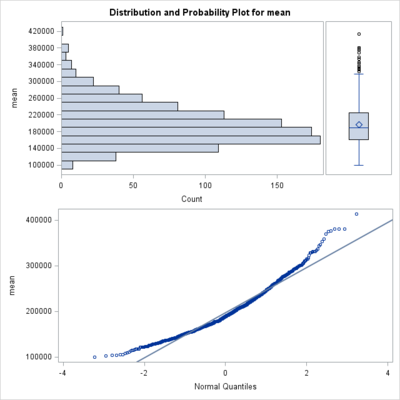
<売上高の平均値の分布>
標本サイズ300の単純無作為抽出を千回実施して、千個の平均値を計算した。下図はそのヒストグラムであり、やや高い方に裾を引いているが正規分布に近づいている様子が分かる。この千個の平均値は1968億円であり、母平均の1979億万円にほぼ一致している。
これが中心極限定理の直観的な可視化である。